Keras – Deep Learning für Einsteiger

Was ist Keras?

Vielen Anfängern fällt es schwer, sich unter den vielen Frameworks für neuronale Netzwerke zu entscheiden. Das liegt nicht zuletzt daran, dass diese Frameworks sehr anspruchsvoll sind (siehe Tensorflow). Womit kann ich also am besten damit anfangen, neuronale Netzwerke zu programmieren? Ganz einfach: Keras!

Keras ist eine High-Level Neural Network API, die in Python entwickelt wurde. Sie baut dabei auf komplexen Frameworks (TensorFlow, Theano oder CNTK) auf. Keras bietet ein enormes Abstraktionslevel der jeweiligen Backends, was nicht nur Anfängern zugute kommt: Besonders zur Entwicklung von Prototypen und zum Testen dieser hat Keras seinen Platz gefunden. Darin zeigt sich jedoch auch der Nachteil von Keras: Als erfahrener Entwickler neuronaler Netzwerke ist man stark eingeschränkt. Zum Beispiel bietet Keras aktuell noch keine Implementierungsmöglichkeit eigener Kostenfunktion.

Wie funktioniert Keras?

https://www.youtube.com/watch?v=j_pJmXJwMLA

Keras macht sich das Baukastenprinzip zunutze: Schichten, die das Netzwerk bekommen soll, werden aneinander gehängt.
Angenommen, man möchte ein Modell realisieren, das einen Text-Input (in Form von Indizes) mit einem LSTM und CNN auswertet, die Ausgaben konkateniert, einem hidden Layer übergibt und mithilfe einer Softmax-Funktion kategorisiert. Dann könnte das folgendermaßen aussehen:

# Embedding Layer, um Vektoren aus den Indizes zu generieren
embedding_layer = Embedding(input_dim = 2000, output_dim =50, weights=[myMatrix])
# Aufbau des Netzwerkes
input = Input(shape=(20,), dtype='int32', name='input')
embedded_input = embedding_layer(input)
conv = Conv1D(20, 3, activation='relu', strides=1)(embedded_input)
conv = MaxPooling1D(pool_size=2)(conv)
conv = Flatten()(conv)
lstm = LSTM(20, return_sequences=True)(embedded_input)
conc = Concatenate()([conv, lstm])
hidden = Dense(30, activation="relu")(conc)
output = Dense(5, activation="softmax", name='output')(hidden)
model = models.Model(inputs=[input], outputs=[output])

Dieses Beispiel ist ziemlich komplex und über die Sinnhaftigkeit kann man sich streiten. Jedoch zeigt es besonders gut, dass beliebige Netzwerkschichten einfach miteinander kombiniert werden können.

Anmerkung: In diesem Beispiel wurde die Functional-API von Keras verwendet, mit der man komplexe Keras-Modelle realisieren kann. Im folgenden Beispiel soll aber ein Problem analysiert werden, für das eine einfache Architektur ausreicht. Dafür bietet Keras eine alternative Herangehensweise an.

Vorverarbeitung und Einlesen des Datensatzes

Alle Dateien können als ZIP heruntergeladen werden: iris_ff_with_keras

In diesem Beispiel kommt der Iris-Datensatz von scikit-learn zum Einsatz.

Features: Kelchblattlänge, Kelchblattbreite, Blütenlänge und Blütenbreite
Typen: Setosa, Versicolour, und Virginica

Scikit-learn stellt verschiedene Datensätze zur Verfügung, die alle auf die gleiche Art und Weise eingelesen werden können:

# Einlesen des Iris Datensatzes 
from sklearn.datasets import load_iris 
iris_dataset = load_iris() 
X = iris_dataset['data'] 
y = iris_dataset['target']

Um einen Einblick in die Daten zu erhalten, lasse ich mir die Anzahl von Datensätzen, sowie konkrete Beispiele ausgeben:

print('Features: {}'.format(X.shape))
print('Ausgabe: {}'.format(y.shape))
# Gib die 10 ersten Datensätze
for ex_x, ex_y in zip(X[:10], y[:10]):
    print('{} -> {}'.format(ex_x, ex_y))
Features: (150, 4)
Ausgabe: (150,)
[5.1 3.5 1.4 0.2] -> 0
[4.9 3. 1.4 0.2] -> 0
[4.7 3.2 1.3 0.2] -> 0
[4.6 3.1 1.5 0.2] -> 0
[5. 3.6 1.4 0.2] -> 0
[5.4 3.9 1.7 0.4] -> 0
[4.6 3.4 1.4 0.3] -> 0
[5. 3.4 1.5 0.2] -> 0
[4.4 2.9 1.4 0.2] -> 0
[4.9 3.1 1.5 0.1] -> 0

Im Datensatz befinden sich 150 Sätze. Die Zielwerte (y) werden mit Integern gekennzeichnet (0, 1, 2). Anhand dieses Einblicks, lassen sich bereits relevante Erkenntnisse für das Training ableiten:

  1. Für y müssen 3 Kategorien differenziert werden. Dazu bietet sich ein One-Hot-Encoding mit Softmax-Klassifizierung an.
  2. Die y-Werte sind aufsteigend von 0 bis 2 sortiert. Trainiert ein neuronales Netzwerk mit diesen Sätzen, konzentriert es sich zu stark auf die einzelnen Klassen und vergisst „Wissen“, das es sich bereits für andere Klassen angeeignet hat. Die Lösung: Die Daten müssen gemischt werden.
  3. Die Wertebereiche der vier Features besitzen alle die gleiche Größenordnung. Eine Normalisierung ist deshalb nicht notwendig.

 

Für die beiden Probleme stellt scikit-learn einfache Lösungen bereit:

# One-Hot-Encoding
from sklearn.preprocessing import OneHotEncoder
onehot_encoder = OneHotEncoder(sparse=False, categories='auto')
y = y.reshape(len(y), 1)
y = onehot_encoder.fit_transform(y)

# Mischen der daten
from sklearn.utils import shuffle
X_shuffled, y_shuffled = shuffle(X, y, random_state=0)

Wenn ich mir nun die ersten 10 Sätze ausgeben lasse, erhalte ich folgendes Ergebnis:

for ex_x, ex_y in zip(X_shuffled[:10], y_shuffled[:10]):
    print('{} -> {}'.format(ex_x, ex_y))
[5.8 2.8 5.1 2.4] -> [0. 0. 1.]
[6.  2.2 4.  1. ] -> [0. 1. 0.]
[5.5 4.2 1.4 0.2] -> [1. 0. 0.]
[7.3 2.9 6.3 1.8] -> [0. 0. 1.]
[5.  3.4 1.5 0.2] -> [1. 0. 0.]
[6.3 3.3 6.  2.5] -> [0. 0. 1.]
[5.  3.5 1.3 0.3] -> [1. 0. 0.]
[6.7 3.1 4.7 1.5] -> [0. 1. 0.]
[6.8 2.8 4.8 1.4] -> [0. 1. 0.]
[6.1 2.8 4.  1.3] -> [0. 1. 0.]

Zur Validierung eines Systems müssen die Daten noch in Trainings- und Validierungsdaten gegliedert werden. Für die Validierung sollen 30% der Daten zur Verfügung gestellt werden und für das Training 70%:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_shuffled, y_shuffled, random_state=0, train_size=0.3)
print("Features Training Shape: {}".format(X_train.shape))
print("Features Test Shape: {}".format(X_test.shape))
Features Training Shape: (45, 4)
Features Test Shape: (105, 4)

Erstellung eines Neuronalen Netzwerks

Für die gegebenen Daten bietet sich ein FF-Network (Feed Forward) an. Dazu habe ich folgende Klasse geschrieben:

from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras import regularizers
from History import TrainingHistory
import numpy
numpy.random.seed(7)

class FeedForward:
    """Einfaches Modell für ein FF-Netzwerk"""

    def __init__(self, input_dim):
        self.model = Sequential()
        self.model.add(Dense(8, input_dim=input_dim, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
        self.model.add(Dense(4, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
        self.model.add(Dense(3, activation='softmax'))
        print(self.model.summary())

Ein Netzwerk kann erzeugt werden, indem man eine Instanz von Sequential erzeugt (Im Gegensatz zur Functional-API). Daraufhin kann man beliebige Netzwerkschichten aneinander reihen. Im ersten Dense-Layer muss die Dimension der Inputs mit input_dim angegeben werden (hier die Anzahl der Features). Der erste Wert jedes Dense-Layers gibt an, wie groß die Folgeschicht ist (Anzahl der Knoten). Mit activation kann man die Aktivierungsfunktionen festlegen. Hier kommt für die ersten beiden Schichten eine Rectified Linear Unit zum Einsatz und für die letzte Schicht eine Softmax-Funktion.

Eine sehr hilfreiche Funktion ist summary(). Damit kann man sich den Aufbau des Modells und Anzahl der Parameter ausgeben lassen.

_________________________________________________
Layer        (type)    Output Shape    Param #
=================================================
main_input   (Dense)   (None, 8)       40
_________________________________________________
hidden_layer (Dense)   (None, 4)       36
_________________________________________________
main_output  (Dense)   (None, 3)       15
=================================================
Total params: 91
Trainable params: 91
Non-trainable params: 0
_________________________________________________

Um das Modell zu trainieren und evaluieren, bekommt die Klasse zwei weitere Funktionen:

    def train(self, X, Y, X_test, y_test):
self.model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
        self.model.fit(
            X, 
            Y, 
            validation_data=(X_test, y_test),
            epochs=50,
            batch_size=4,
            verbose=1
        )

    def evaluate(self, X, Y):
        scores = self.model.evaluate(X, Y)
        print('{}: {}%'.format(self.model.metrics_names[1], round(scores[1]*100, 2)))

Mit dem stochatischen Gradientenverfahren wird das Modell 400 Epochen trainiert. Nun kann das Modell vollständig aufgebaut, trainiert und evaluiert werden:

from myModels import FeedForward
model = FeedForward(4)
model.train(X_train, y_train, X_test, y_test)
model.evaluate(X_test, y_test)

45/45 [==============================] - 0s 369us/step - loss: 0.7282 - acc: 0.8444 - val_loss: 0.7376 - val_acc: 0.8381
Epoch 49/50
45/45 [==============================] - 0s 412us/step - loss: 0.7175 - acc: 0.8222 - val_loss: 0.7253 - val_acc: 0.8286
Epoch 50/50
45/45 [==============================] - 0s 369us/step - loss: 0.7072 - acc: 0.8222 - val_loss: 0.7197 - val_acc: 0.8571
acc: 85.71%

Mit dieser Konfiguration erreicht das Modell im Test eine Accuracy von 85.71%. Das ist noch nicht besonders gut. Es gilt, das Modell zu analysieren, um Möglichkeiten zur Verbesserung zu finden.

Analyse der Resultate

Um die Resultate zu analysieren lohnt es sich, den Verlauf von Loss und Accuracy pro Epoche zu betrachtet. Um auf diese Werte zuzugreifen, stellt Keras Callbacks zur Verfügung, die Auf Zwischenergebnisse vor, während und nach einer Epoche zugreifen können. Dazu habe ich folgende Klasse geschrieben:

from keras.callbacks import Callback
class TrainingHistory(Callback):
    def __init__(self):
        self.val_acc = []
        self.acc = []
        self.val_loss = []
        self.loss = []

    def on_train_begin(self, logs={}):
        self.train_accs = []
        self.val_accs = []

    def on_epoch_end(self, epoch, logs={}):
        self.acc.append(logs.get('acc'))
        self.val_acc.append(logs.get('val_acc'))
        self.val_loss.append(logs.get('val_loss'))
        self.loss.append(logs.get('loss'))

Um Callbacks einzubinden, muss die FeedForward-Klasse angepasst werden:

    def __init__(self, input_dim):
        self.model = Sequential()
        self.model.add(Dense(8, input_dim=input_dim, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
        self.model.add(Dense(4, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
        self.model.add(Dense(3, activation='softmax'))
        self.callback = TrainingHistory()
        print(self.model.summary())

    def train(self, X, Y, X_test, y_test):
        self.model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
        self.model.fit(
            X,
            Y,
            validation_data=(X_test, y_test),
            epochs=50
            batch_size=4,
            verbose=1,
            callbacks=[self.callback]
        )

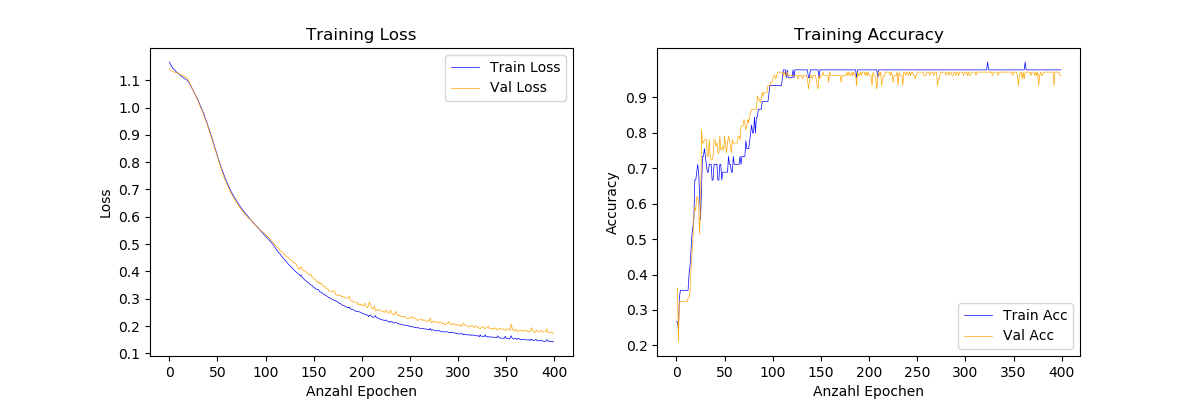
Unter Zuhilfenahme von Matplotlib können Accuracy und Loss bezüglich der Epochen visualisiert werden. Dazu habe ich eine weitere Klasse geschrieben (s. Projekt). Um den Graphen zu erzeugen, wird folgender Code ausgeführt:

from Graphs import ComparisonGraph
import matplotlib.pyplot as plt
call = model.callback
acc_graph = ComparisonGraph(len(call.acc), call.loss, call.val_loss, call.acc, call.val_acc)
acc_graph.draw()

Training und Validierung erreichen ähnlich gute Ergebnisse. Das heißt, man könnte das Modell komplexer gestalten, sowie die Trainingszeit erhöhen. Die beste Konfiguration, die ich erreichen konnte, trainiert 400 Epochen lang und hat folgenden Aufbau:

self.model = Sequential()
self.model.add(Dense(8, input_dim=input_dim, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
self.model.add(Dense(6, activation='relu', kernel_regularizer=regularizers.l2(0.01)))
self.model.add(Dense(3, activation='softmax'))
Das Modell erreicht nun eine Accuracy von 97.14%.
Wer jetzt glaubt, man müsse 100% erreichen, sollte niemals vergessen, dass diese Netzwerke nicht dazu ausgelegt sind! Es existieren immer Ausreißer, die unser Modell nicht erkennen kann. Aus diesem Grund können wir mit einer Accuracy von 97.14% sehr zufrieden sein.

Kommentare sind geschlossen